包含Lecture 6、7、8
Lecture 6&7
①线性(liner)递归、尾递归(tail)、树递归(tree)
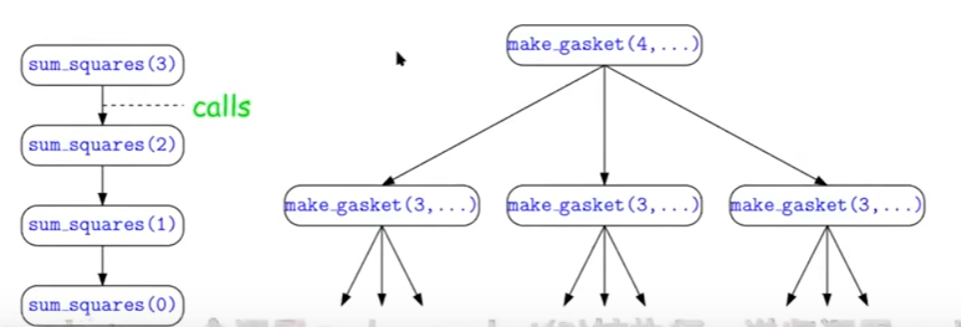
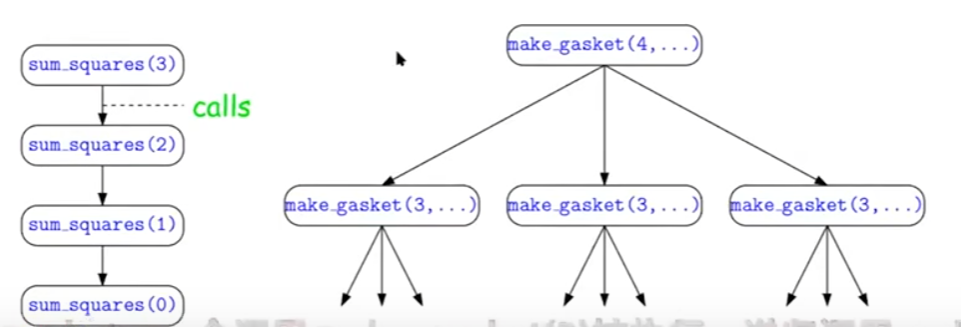
如图,左边为线性递归,右边为树递归,其区别就在于每个函数体中是否递归多次。
尾递归是线性递归的一种。仅return且不进行其他操作的线性递归函数可被视为尾递归。大部分线性递归都是尾递归。
②递归原则问题——避免无限递归
无限递归的简单举例:走迷宫问题中如果可以同时走向左/向右两个方向,不做处理就在两个方向上做递归,就会发生无限递归。

要防止出现这种无限递归的情况,需要保证每下一次递归的输入小于上一次的输入,从各种意义上来说。
PS:当然对于迷宫问题可以对走过的位置进行记录
③分割计数问题

题目大意:n为分割原数,k为最大的分割出的数字(简称割数),求分割方法总数。
要用递归解决这个问题,我们能很容易想到树递归。接着就会面临两个问题:
返回条件?返回值?
怎样分割才能覆盖到全部情况而不重复?
首先就要观察题目,并且发现两种分割的方法:

一种是将k作为最大整数直接分割出一部分,然后再递归地分割n-k的部分;
一种是分割出小于k的整数,也就是分割(n,k-1),再分割(n-(k-1),k-1)。
于是我们不难看出,在分割的过程中:
n和k的值均在变小,为了符合之前提到的递归原则,应该设置一个边界值。n<=0时应该return 0来阻止进一步分割。k==1时,说明只能将n拆成n个1,这时就自然只有一种解法,所以就该return 1。
两种分割方法应该分别对应树递归的两个部分,即分割(n-k,k)和(n,k-1),且方法总数应该为树递归之和。
那么递归的函数也就迎刃而解了。

PS:个人感觉这种分割方法需要一个很巧妙的构思来推出。多理解这个案例可能会对加深递归的理解有帮助。
Lecture 8
①异常(Exception)
当客户(clinet)不按照函数的规定方法调用函数时,程序员可以通过抛出异常的方式终止程序,并将异常正式地提出。
提出异常的方法是raise或assert。一般来说assert是raise的外包装,出现assert说明程序出现了很糟糕的错误。

一般来说程序员可以在某些地方预知到客户的错误操作,就可以使用try/except语句来抛出自定义的错误,并且防止程序不当地终止运行。

你可以在try的前一个缩进里写上while循环,并且恰当地控制条件,就能得到一个只有输入正确才能正确运行的程序块。
②书写递归函数的哲学
- 在函数开始时先写注释。标注基本的边界情况,说明函数的功能,给出一些具体的I/O案例。
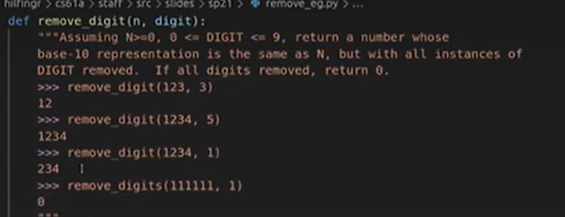
从边界情况开始考虑。一些边界情况往往也就是递归尾部时的返回,将其考虑清楚能很大程度上奠定一个递归函数能够正确运行的基础。
将自然语言翻译成程序语言,并且递归地执行函数。
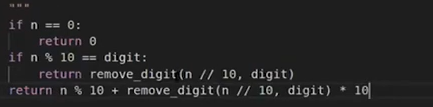
小技巧
1、python -i进入交互模式,可以在此模式下随意调用函数,进行一些方便的调试操作。
2、
1
2
3
| if __name__ == "__main__":
import doctest
doctest.testmod()
|
用以上代码实现自动代码检测。
作业
①lab03
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| HW_SOURCE_FILE = __file__
def summation(n, term):
"""Return the sum of numbers 1 through n (including n) w��th term applied to each number.
Implement using recursion!
>>> summation(5, lambda x: x * x * x) # 1^3 + 2^3 + 3^3 + 4^3 + 5^3
225
>>> summation(9, lambda x: x + 1) # 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
54
>>> summation(5, lambda x: 2**x) # 2^1 + 2^2 + 2^3 + 2^4 + 2^5
62
>>> # Do not use while/for loops!
>>> from construct_check import check
>>> # ban iteration
>>> check(HW_SOURCE_FILE, 'summation',
... ['While', 'For'])
True
"""
assert n >= 1
"*** YOUR CODE HERE ***"
if n == 1:
return term(n)
else:
return term(n)+summation(n-1,term)
def pascal(row, column):
"""Returns the value of the item in Pascal's Triangle
whose position is specified by row and column.
>>> pascal(0, 0)
1
>>> pascal(0, 5) # Empty entry; outside of Pascal's Triangle
0
>>> pascal(3, 2) # Row 3 (1 3 3 1), Column 2
3
>>> pascal(4, 2) # Row 4 (1 4 6 4 1), Column 2
6
"""
"*** YOUR CODE HERE ***"
if row - column < 0 or column < 0 or row < 0:
return 0
elif column == row or column == 0:
return 1
else:
return pascal(row-1,column)+pascal(row-1,column-1)
def compose1(f, g):
""""Return a function h, such that h(x) = f(g(x))."""
def h(x):
return f(g(x))
return h
def repeated(f, n):
"""Returns a function that takes in an integer and computes
the nth application of f on that integer.
Implement using recursion!
>>> add_three = repeated(lambda x: x + 1, 3)
>>> add_three(5)
8
>>> square = lambda x: x ** 2
>>> repeated(square, 2)(5) # square(square(5))
625
>>> repeated(square, 4)(5) # square(square(square(square(5))))
152587890625
>>> repeated(square, 0)(5)
5
>>> from construct_check import check
>>> # ban iteration
>>> check(HW_SOURCE_FILE, 'repeated',
... ['For', 'While'])
True
"""
"*** YOUR CODE HERE ***"
if n == 1:
return f
elif n == 0:
return lambda x: x
else:
return compose1(f,repeated(f,n-1))
|
前两题都是儿简送。
最后一题我是先写了n==1的边界情况,然后试探着摸了递归式,意外地一次性过了!
但是爆了最后一个测试点:repeated(square, 0)(5),也就是n==0时候的情况。
由于函数的调用方法就是后面再加一个括号,所以n==0时候我们也得返回一个函数。n==0代表不执行这个函数,那么就应该直接返回x值,写个lambda即可。
用时大约1h
②disc03
第一题做傻了,不做了,免得不想学了
趣事
1

2